Площади двух участков поля находятся в отношении 3 : 8. Какова площадь (в гектарах) меньшего участка поля, если общая площадь двух участков равна 682 га?
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Некоторое количество рабочих одинаковой квалификации выполнили работу за 14 дней. Если бы их было на 12 человек больше и каждый работал на 1 час в день дольше, та же работа была бы сделана за 10 дней. Если бы рабочих было еще на 18 человек больше и каждый работал еще на 1 час в день дольше, то эта работа была бы сделана за 7 дней. Найдите исходное количество рабочих.
Через электронный сервис Маша купила билет на концерт и заплатила 80 руб. В эту сумму входит стоимость билета и сервисный сбор 4 руб. За неделю до концерта Маша-решила вернуть билет. По правилам организатора концерта ей вернут не менее 75% стоимости билета. Какую наибольшую сумму (в рублях) может потерять Маша, вернув билет?
Через электронный сервис Маша купила билет на концерт и заплатила 72 руб. В эту сумму входит стоимость билета и сервисный сбор 4 руб. За неделю до концерта Маша решила вернуть билет. По правилам организатора концерта ей вернут не менее 75% стоимости билета. Какую наибольшую сумму (в рублях) может потерять Маша, вернув билет?
Из города А в город В, расстояние между которыми 100 км, одновременно выезжают два автомобиля. Скорость первого автомобиля на 10 км/ч больше скорости второго, но он делает в пути остановку на 50 мин. Найдите наибольшее значение скорости (в км/ч) первого автомобиля, при движении с которой он прибудет в В не позже второго.
У Юры есть некоторое количество марок, а у Яна марок в 2 раза больше, чем у Юры. Мальчики поместили все свои марки в один альбом. Среди чисел 26; 38; 20; 37; 39 выберите то, которое может выражать количество марок, оказавшихся в альбоме.
В каждую из трех корзин положили одинаковое количество яблок. Если в одну из корзин добавить 19 яблок, то в ней их окажется меньше, чем в двух других корзинах вместе. Если же в эту корзину положить еще 23 яблока, то в ней их станет больше, чем было первоначально в трех корзинах вместе. Сколько яблок было в каждой корзине первоначально?
Велосипедист за 5 ч проехал 52 км. За какое время (в минутах) велосипедист преодолеет в полтора раза больший путь, если будет двигаться с той же скоростью?
Из пунктов A и B, расстояние между которыми 160 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта A до места встречи автомобилей.
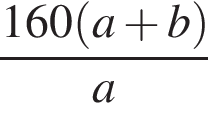
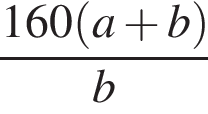
Из пунктов А и В навстречу друг другу одновременно выезжают мотоциклист и велосипедист с постоянными и неравными скоростями и встречаются через t часов. Укажите формулу, по которой можно определить скорость v (км/ч) мотоциклиста, если известно, что расстояние AB равно S км и велосипедист проехал его за a часов.
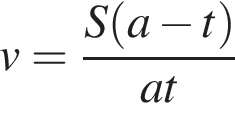
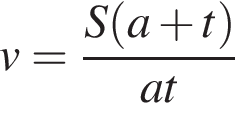
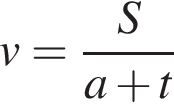
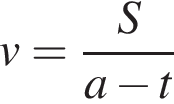
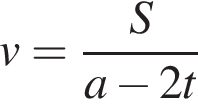
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
На одной чаше уравновешенных весов лежат 3 яблока и 1 груша, на другой — 2 яблока, 2 груши и гирька весом 20 г. Каков вес одного яблока (в граммах), если все фрукты вместе весят 780 г? Считайте все яблоки одинаковыми по весу и все груши одинаковыми по весу.
Велосипедист за 6 ч проехал 58 км. За какое время (в минутах) велосипедист преодолеет в полтора раза больший путь, если будет двигаться с той же скоростью?
Площади двух участков поля находятся в отношении 4 : 7. Какова площадь (в гектарах) менышего участка поля, если общая площадь двух участков равна 495 га?
Собственная скорость катера в 9 раз больше скорости течения реки. Расстояние по реке от пункта A до пункта B плот проплыл за время t1, а катер — за время t2. Тогда верна формула:
В двух сосудах 57 литров жидкости. Если 5% жидкости из первого сосуда перелить во второй, то в обоих сосудах окажется одинаковое количество жидкости. Сколько литров жидкости было во втором сосуде первоначально?
Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?
За n коробок конфет было заплачено 152 руб. 20 коп., а за n коробок печенья — b руб. Составьте выражение, которое определяет, на сколько копеек коробка печенья дешевле коробки конфет.
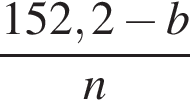
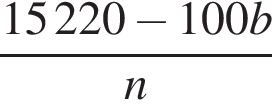
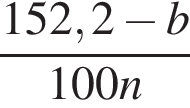
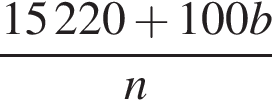
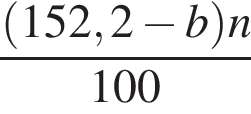
Автомобиль проехал некоторое расстояние, израсходовав 21 л топлива. Расход топлива при этом составил 9 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 12 л на 100 км. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Две снегоочистительные машины, работая одновременно, очистили всю улицу за 24 мин. Если бы половину улицы очистила первая машина, а затем оставшуюся часть улицы — вторая машина, то вся улица была бы очищена за 50 мин. За какое время (в минутах) вторая машина, работая одна, очистила бы всю улицу, если известно, что она работает медленнее, чем первая машина?
Два крана, работая одновременно, разгрузили баржу за 9 ч. Если бы половину баржи разгрузил первый кран, а затем оставшуюся часть — второй кран, то баржа была бы разгружена за 50 ч. За какое время (в часах) первый кран, работая один, разгрузил бы всю баржу, если известно, что он работает медленнее, чем второй кран?

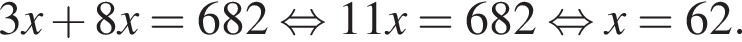
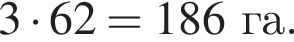
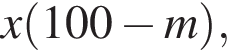 во втором —
во втором — 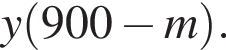 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 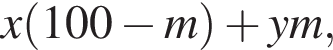 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: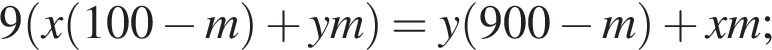
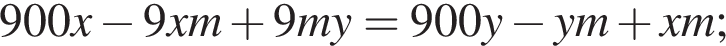

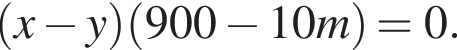

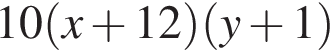 единиц продукции.
единиц продукции.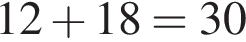 больше и они трудились на два часа дольше каждый день, то произвели бы за 7 дней
больше и они трудились на два часа дольше каждый день, то произвели бы за 7 дней  единиц продукции.
единиц продукции.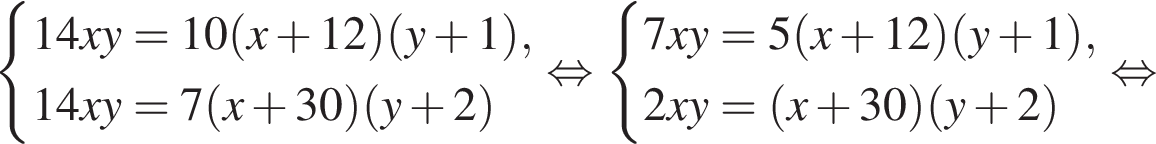
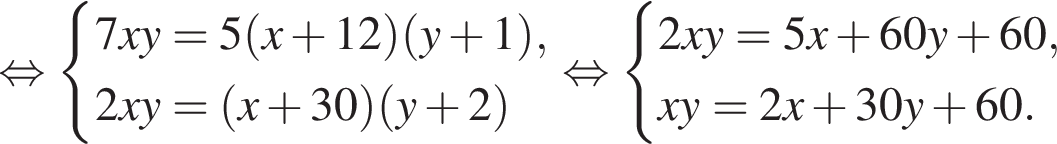
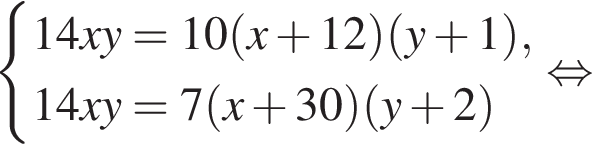
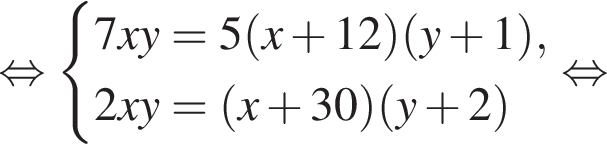
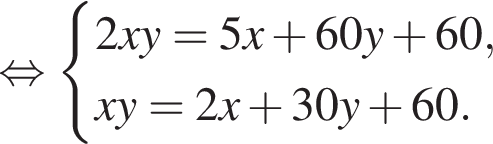
 или x = 60. Тогда второе уравнение дает
или x = 60. Тогда второе уравнение дает 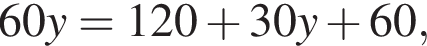 откуда
откуда  или
или  Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 23 руб.
Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 23 руб. Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 21 руб.
Деньги, уплаченные за сервисный сбор, Маше не вернут, таким образом, наибольшая сумма, которую Маша может потерять, вернув билет, равна 21 руб.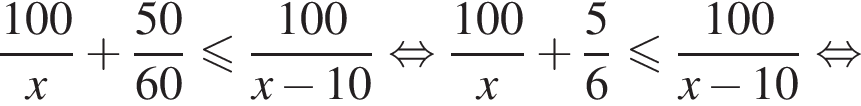

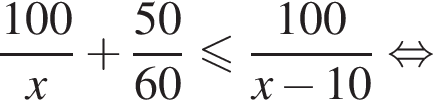
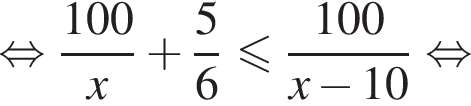
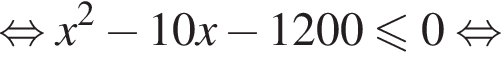

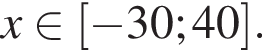 Таким образом, наибольшее значение скорости первого автомобиля — 40 км/ч.
Таким образом, наибольшее значение скорости первого автомобиля — 40 км/ч.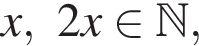 общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.
общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.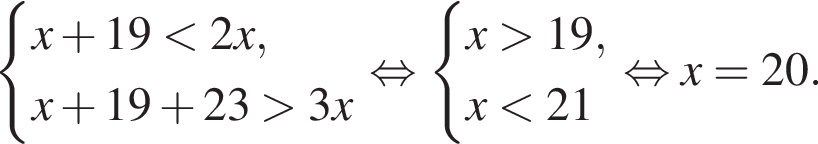
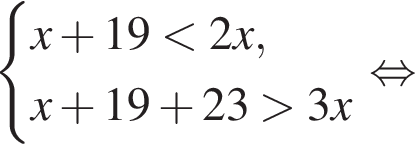
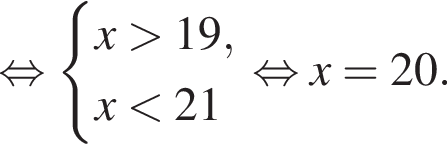
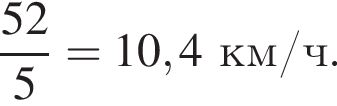 Если длину пути увеличить в полтора раза, велосипедист преодолеет путь за
Если длину пути увеличить в полтора раза, велосипедист преодолеет путь за 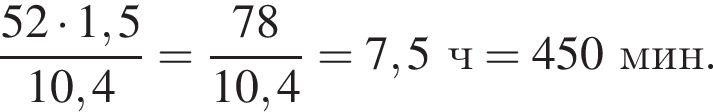
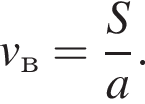 Скорость сближения мотоциклиста и велосипедиста равна
Скорость сближения мотоциклиста и велосипедиста равна 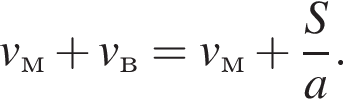 Тогда
Тогда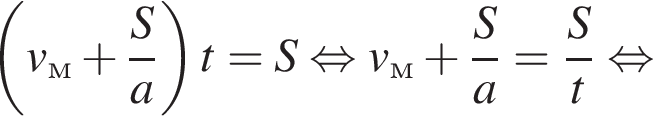
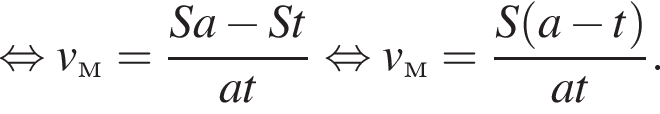
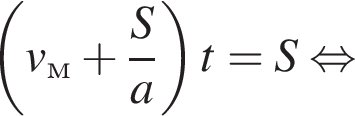
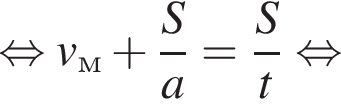
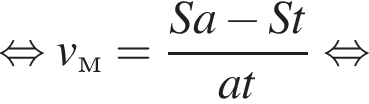
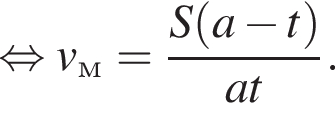
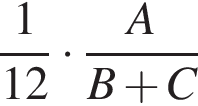 работы.
работы. 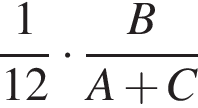 работы.
работы. 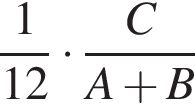 работы.
работы. 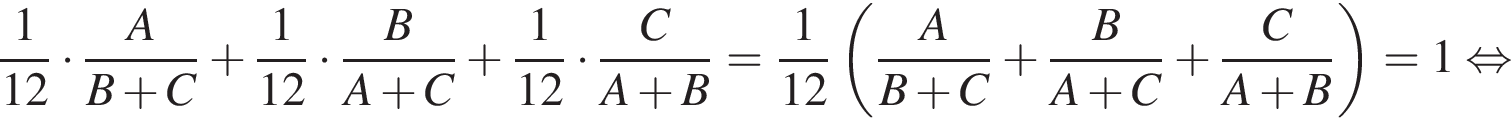
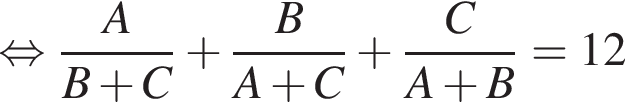
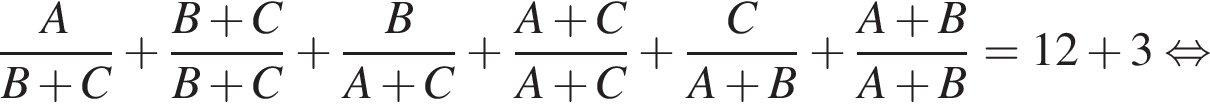
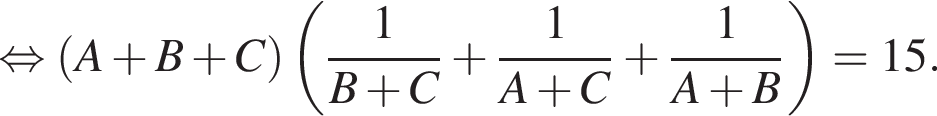
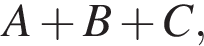 то они выполнили бы работу за:
то они выполнили бы работу за: 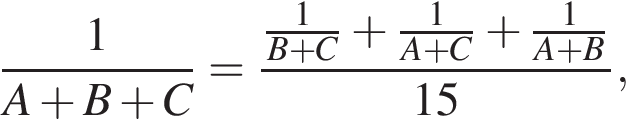
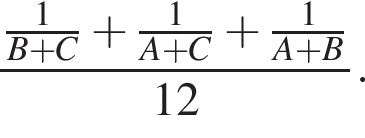 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 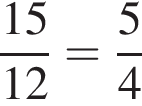 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число 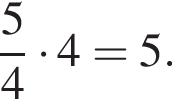
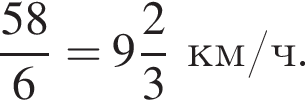 Если длину пути увеличить в полтора раза, велосипедист преодолеет путь за
Если длину пути увеличить в полтора раза, велосипедист преодолеет путь за 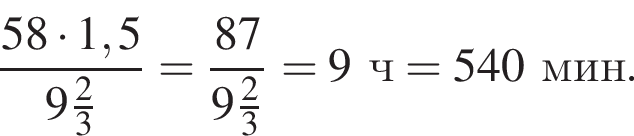
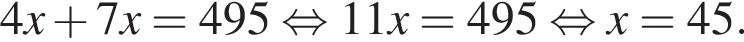
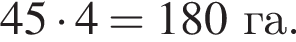
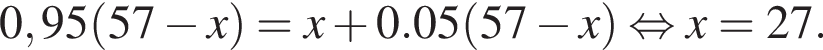


 Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 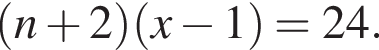 Решим систему уравнений:
Решим систему уравнений: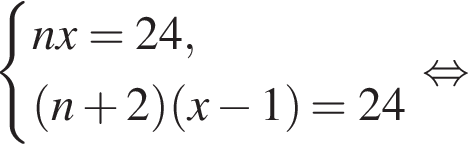
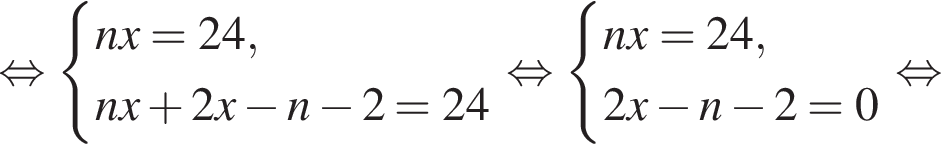
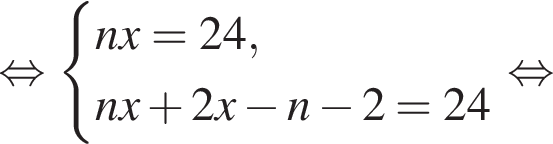
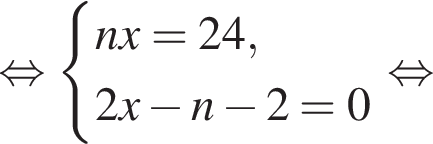
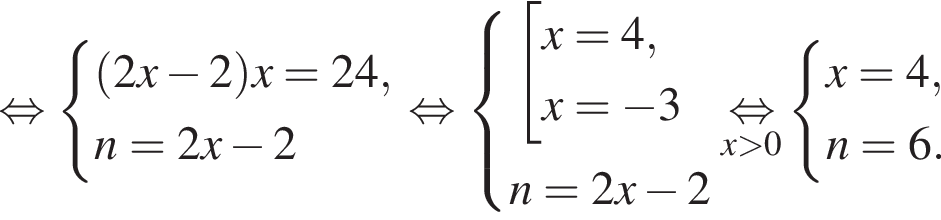
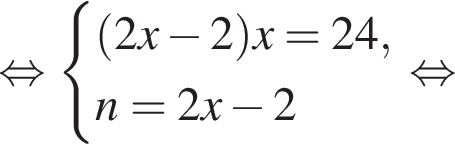
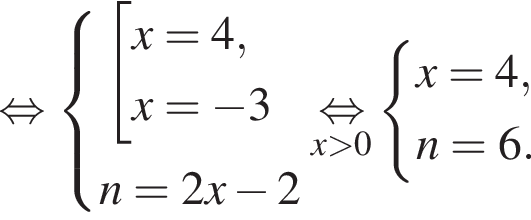
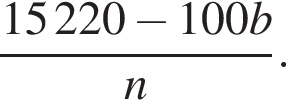
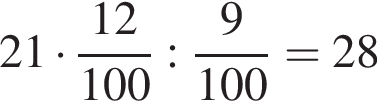 л.
л.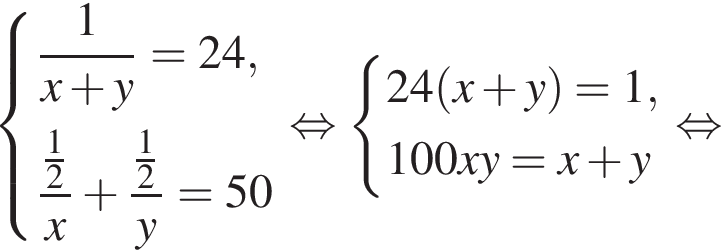
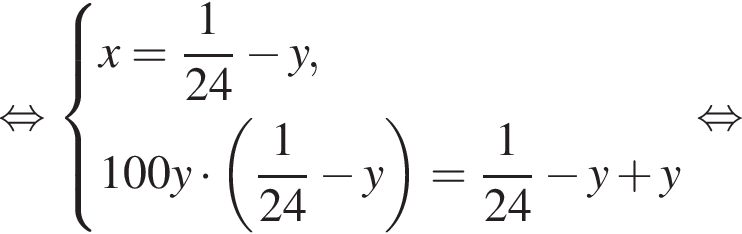
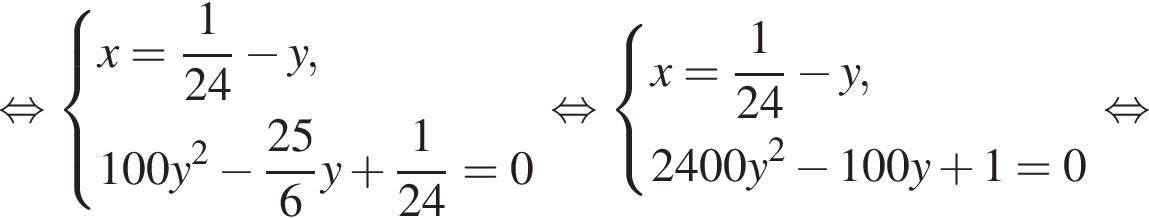
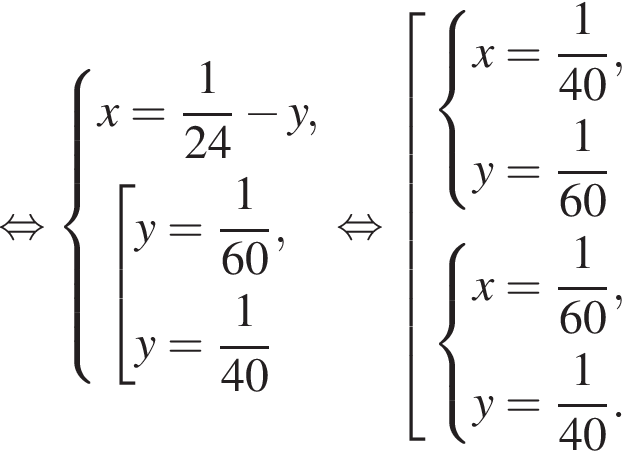
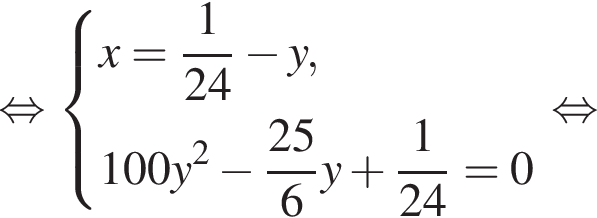
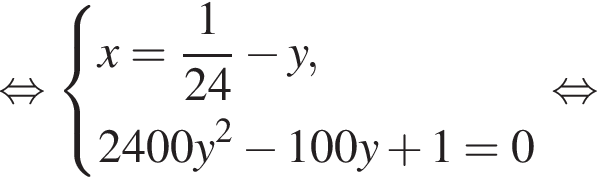
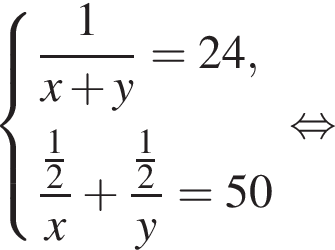
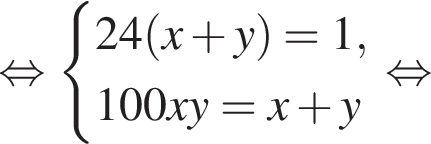
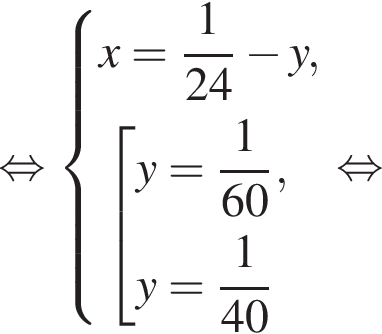
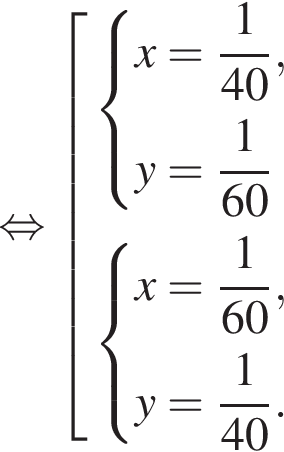
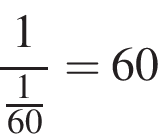 минут.
минут.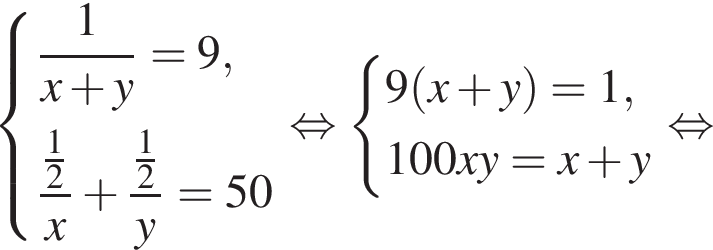
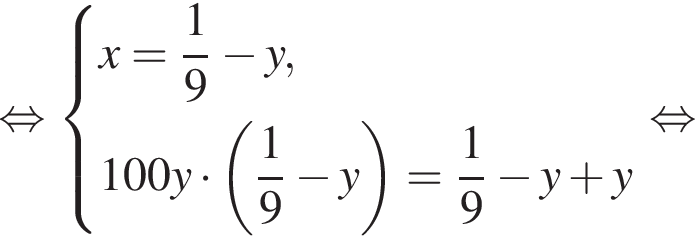
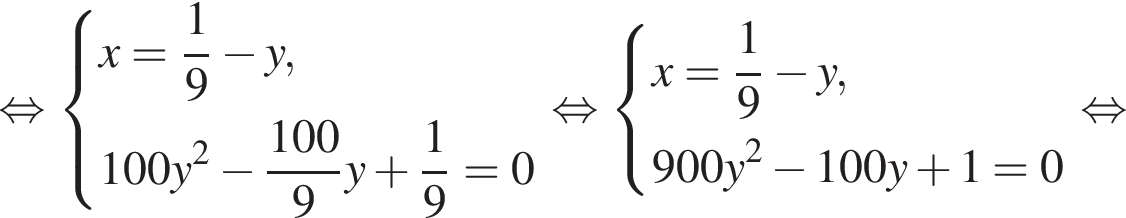
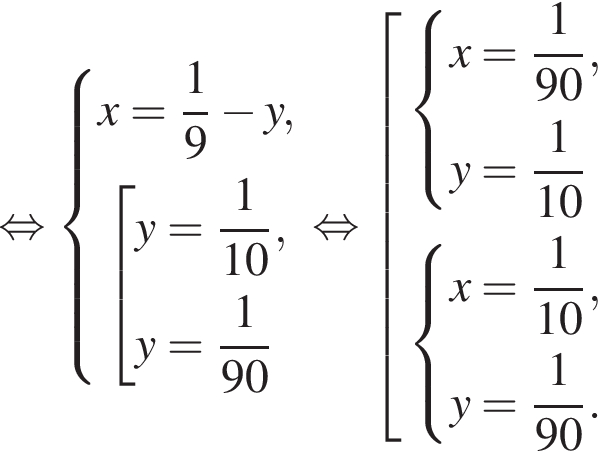
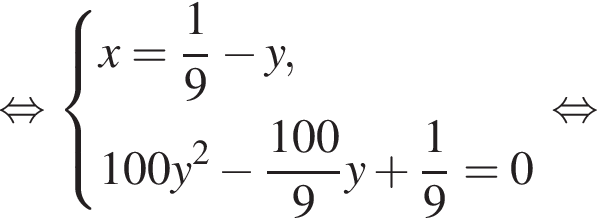
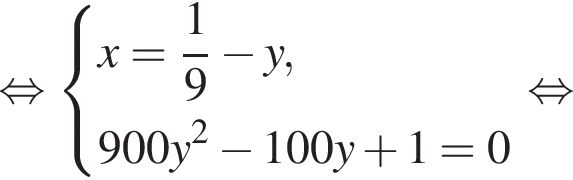
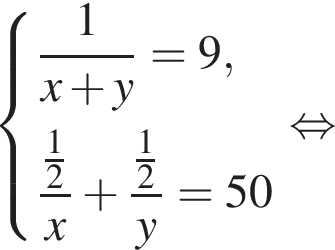
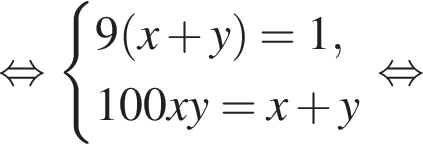
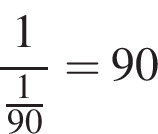 часов.
часов.